Objem kvádru y se matematicky vyjadřuje rovnicí

y = x (S – 2x) (V – 2x),
kde x je délka strany odstřihnutých rohů archu, S a V jsou šířka resp. výška archu, jejichž velikosti jsou uvedeny v zadání úlohy. Rovnici rozepíšeme, aby se další matematické úkony snadněji prováděly
y = 4x³ – 2x²(S + V) + xSV

Extrémní hodnotu y znázorňuje tangenta, která svírá nulový úhel s osou x.
Tangenta extrému y se nachází tam, kde derivace y podle x se rovná 0.
dy/dx = 0 = 12x² – 4x(S +V) + SV
To je kvadratická rovnice, která pro x vykazuje dva kořeny, tudíž y má dva extrémy.

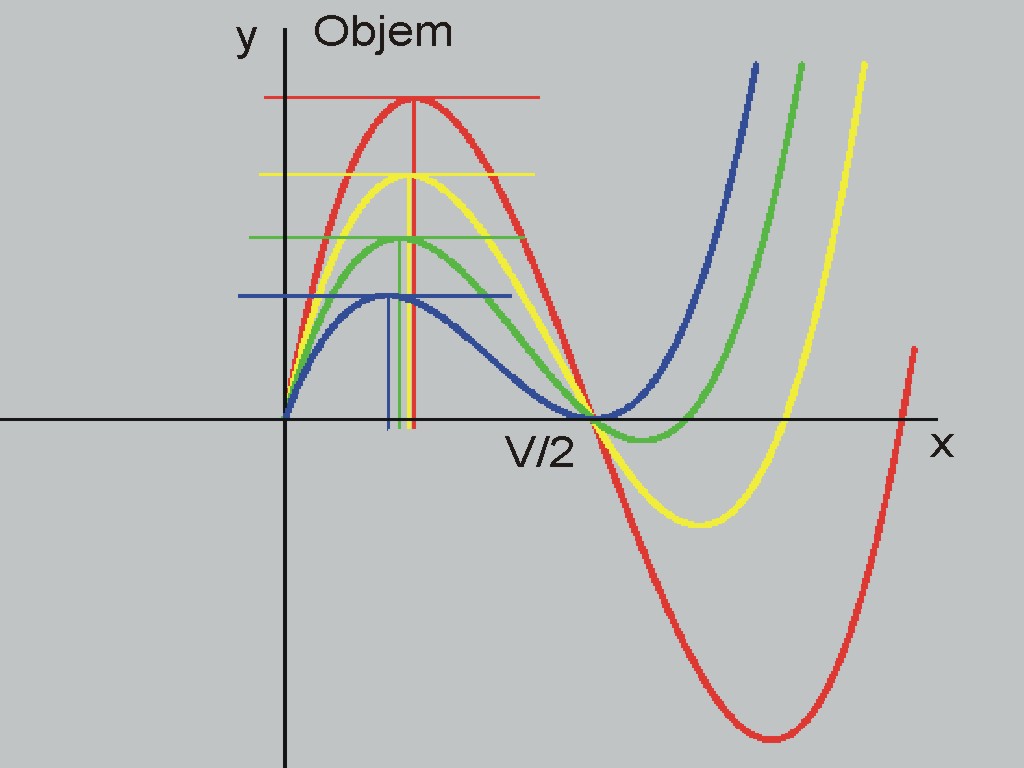
Obr.2 Rovnice objemu y = x (S – 2x) (V – 2x) pro x v mezích 0 < x < ∞
(kvadr.exe)

Grafický obraz rovnice y a tangenty v kladném extrému jsou znázorněny na Obr. 2. Pro každou hodnotu výšky archu V můžeme odstřihnout jen čtverečky kusů o maximální velikosti strany x = V/2, pak objem kvádru má nulovou hodnotu. Zbytek archu je menší arch.

Objem vykazuje dva extrémy – jeden kladný, druhý záporný. Záporný objem neexistuje podle zdravého rozumu, a tak použitelný je kladný extrém objemu, kde je znázorněna také tangenta. Matematice však nic nebrání znázornit y i pro další kladné hodnoty x. Tu se ukazuje první rozpor mezi zdravým rozumem a matematikou. Dřív než si tento rozpor objasníme a vysvětlíme v čem je rozdíl mezi zdravým rozumem a matematikou, uveďme ještě další možnosti matematiky.

Obr.3 Rovnice objemu y = x (S – 2x) (V – 2x) pro x v mezích –∞ < x < ∞
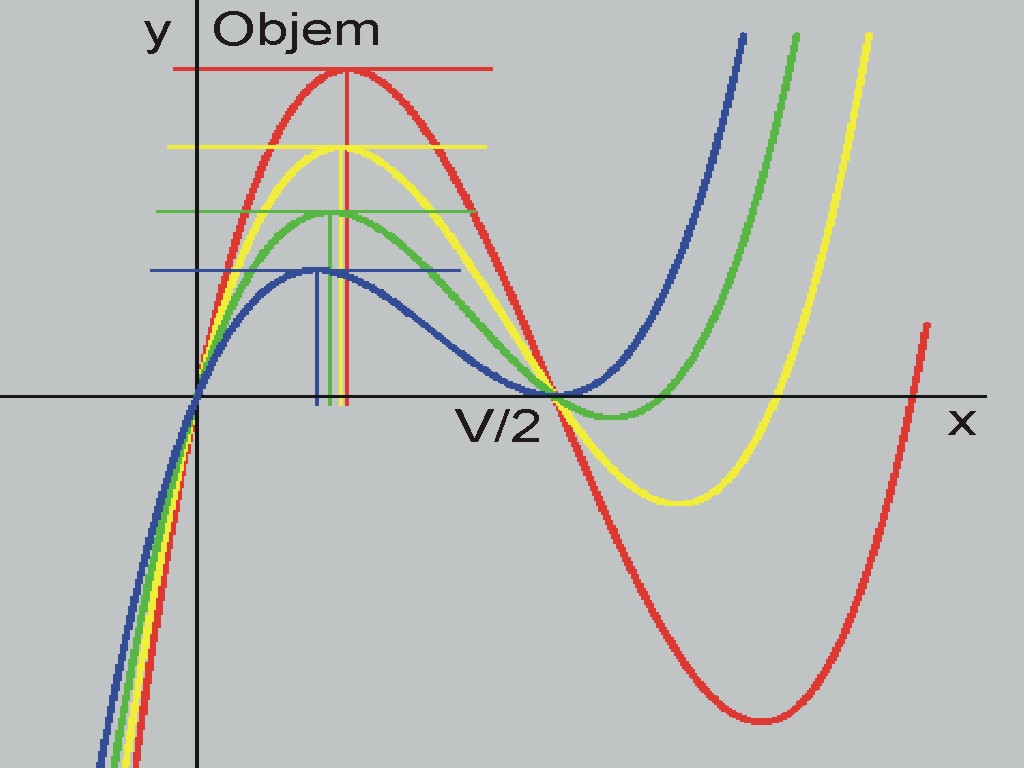
Rovnice objemu y je znázorněna i pro záporné hodnoty x, což podle zdravého rozumu není možné.
( Kvadr.exe)

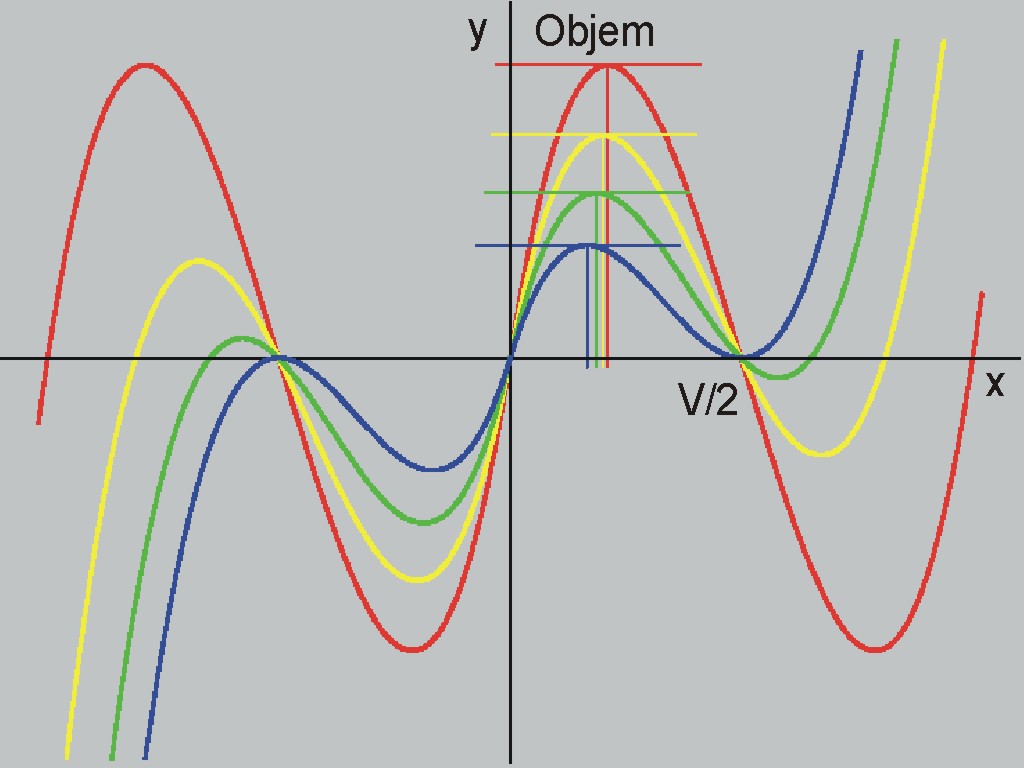
Obr.4 Rovnice objemu je y = x (S – 2x) (V – 2x) když x > 0 a také pro

y = x (–S + 2x) (–V + 2x) když x < 0

(Kvadr.exe)

Na rozdíl od Obr. 3 předpokládáme na Obr. 4, že pro záporné hodnoty x existuje záporný arch papíru, což podle zdravého rozumu není možné, ale matematika to umožňuje. Graf objemu y pro hodnoty x < 0 a graf objemu y pro hodnoty x > 0 jsou zrcadlové obrazy nejdřív podle osy y a pak podle x.

Po tomto předvedení možností matematiky vysvětlíme, v čem spočívá rozdíl mezi zdravým selským rozumem a matematikou.

Zdravý selský rozum se u člověka vytváří od útlého věku na základě objevování přírodních jevů pomocí smyslových orgánů: očí, uší, nosu atd. V pozdějším věku člověk získává poznatky studiem na škole a čtením knih. Nicméně smyslové orgány člověka jsou omezeny – ptáci mají lepší vidění, divoká zvěř lepší slyšení atd. I když moderní přístroje – mikroskopy, mikrofony atd. rozšiřují možnosti lidských smyslů, podstatné je, že pojmy, které jsou stavebním kamenem zdravého rozumu člověka, mají konkrétní fyzikální obsah. Vysloví-li se slovo např. jablko, vždy se nám vybaví jablíčko a ne nějaký meloun.

Matematika má také své pojmy jako je např. číslo, proměnná, vektor, matice atd. Podstatné je, že tyto pojmy nemají konkrétní fyzikální obsah. Matematika zkoumá jenom vzájemný vztah mezi pojmy. V rovnici y = x (S – 2x) (V – 2x) zkoumá jenom, jakých hodnot může proměnná y nabýt ve vztahu s ostatními pojmy v rovnici. Konkrétní fyzikální význam těmto pojmům a výsledkům matematických bádání pak dodatečně přidá člověk podle svého zdravého rozumu.

Na závěr těchto úvah o vztahu zdravého rozumu a matematiky dodejme, že grafy na Obr. 2 až Obr. 4 vyhodnocoval svým zdravým rozumem amatér (slovo je latinského původu slova amator – milovník). Někdy se vyplatí více důvěřovat matematice a hledat vysvětlení k zamítnutým výsledkům.

Uveďme klasický příklad objevení antihmoty. Významný fyzik Paul Dirac studoval z pozic kvantové relativistické mechaniky pohyb elektronu a odvodil rovnici. Její řešení má dva výsledky – jeden kladný, druhý záporný. Kladný výsledek by amatér připsal elektronu, záporný by označil za nepoužitelný. Ne tak Dirac, který důvěřoval matematice a hledal vysvětlení pro záporný výsledek. Došel k závěru, že existuje do té doby neznámá mikro částice a předpověděl, že existuje částice s hmotností jako elektron, ale s kladným elektrickým nábojem. Svou předpověď publikoval v roce 1928 a v roce 1933 byl poctěn Nobelovou cenou. Diracovu částici objevil v kosmickém záření C. D. Anderon a Nobelovu cenu za objev obdržel v roce 1936.

Dirac bádal a pátral po přírodních zákonech

a jediný „nástroj“, který k tomu měl byla matematika. Nezkoumal a nenavrhoval lidské artefakty jako např. kvádr vytvořený z archu papíru. Tam si vystačíme s rozvinutým zdravým selským rozumem.

Povzbuzeni Dirackovým příkladem, žertem si dovolujeme říct, že rovnice objemu pro záporné hodnoty x a záporný arch papíru (Obr. 4) má fyzikální význam. Objevili jsme záporný papír a čekáme jen na výrobce, který ho vyrobí a dá mu název, nejlépe řeckého původu.

Připomeňme si ještě jeden slavný vědecký výkon, kde matematika slavila triumf. V první polovině 19. století poslední známou planetou v sluneční soustavě byl Uran. Z astronomických pozorování se vědělo, že planeta se nepohybuje přesně po vypočítané dráze podle Newtonových zákonů. Byly chybné tyto zákony? Uznávaný astronom a matematik Leverrier jím pevně věřil a z vyhodnocení odchylek pohybu Uranu od vypočítaných hodnot dospěl k přesvědčení, že existuje do té doby neznámé astronomické těleso, které svou gravitaci odchylku způsobuje. Leverrier informoval astronoma Galleho, kde by se mělo neznámé těleso na obloze nacházet. Galle tam těleso skutečně uviděl a nová planeta dostala jméno Neptun.

A do třetice, E. L. Planckovi se matematickým „klíčem“ povedlo proniknout k jednomu z nejutajovanějších přírodních zákonů, ke kvantovému vyzařovacímu zákonu, který pak spustil lavinu nových přírodních a technických objevů. Připomeneme si je v závěreční kapitole.

Rok 1900 byl začátkem nejen nového století, ale i nebývalého pokroku v poznání zákonů přírody. Od pradávna myslitelé počítali s tím, že energie může nabýt jakýchkoli hodnot – že vykazuje spojité spektrum. Na základě studia záření tepla z černé díry a porovnáním klasické teorie záření s experimentem, objevil Planck kvantovou podstatu energie záření, a tak položil základy bádání přírody na základě kvantové teorie. Ve stávající kapitole uvedeme kroky, které vedou k Planckovu vyzařovacímu zákonu [1].

Obr.5 Černá díra

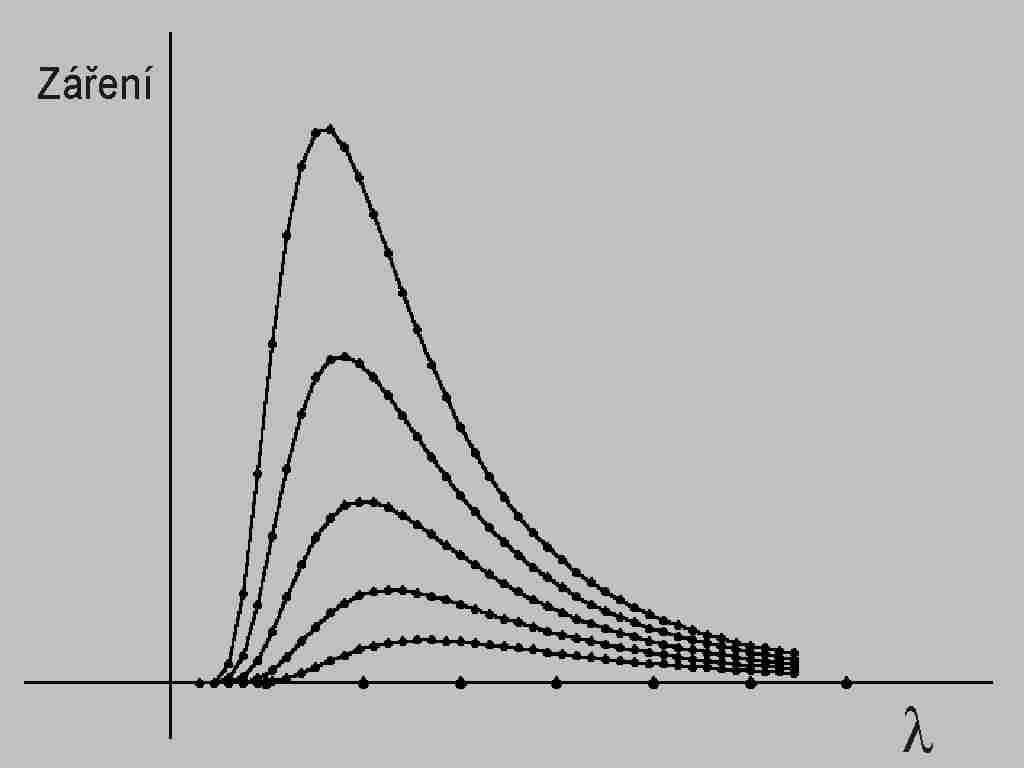
Obr.6 Grafické znázornění Planckova vyzařovacího zákona E_0λ od vysokých k nízkým teplotám.

(
Planck.exe )

Dle klasické statistiky zářivost uzavřené dutiny je dána rovnicí E_0λ = 2πcw*/λ⁴, kde c je rychlost světla, w* střední hodnota energií všech zářičů rozložených po vnitřní stěně dutiny a λ je vlnová délka záření. Tato rovnice, která vychází z předpokladu spojitého spektra vlnových délek, dává dobrou shodu s experimentem pro obor krátkých nebo dlouhých vlnových délek λ. V oblasti mezi těmito obory délek vln není shoda s experimentem. Shodu s experimentem Planck dosáhl teorií, podle které emise a absorpce zářivé energie může probíhat jen po celistvých násobcích kvanta ε = h.f , kde f je vlastní frekvence zářiče (zářivé energie) a h je Planckova konstanta h = 6,624×10^–24[Js].

Celkový počet zářičů je n. Pravděpodobnost, že zářiče emitují energii w_s, označme p_ws, přičemž s nabývá hodnoty s = 1, 2, 3……n. Z teorie klasické statistiky vyplývá p_ws = ae^–sε/kT , kde a je hodnota společná všem zářičům a k je Boltzmannova konstanta k = 1.380….×10^–23 [J/K], která vyjadřuje množství energie potřebné k zahřátí jedné částice ideálního plynu o jeden kelvin.

Počet zářičů s energii w_s je tedy n _s = nae^–sε/kT

a úhrnná energie W všech zářičů je:

Jelikož zářičů v černé díře je nespočetné množství, neděláme prakticky chybu, když počet všech zářičů n v rovnicích považujeme za nekonečný z matematických důvodů. Kvůli zjednodušení psaní následujících rovnic zavedeme označení x = ε/kT a tak bude
n_s = na e^–sx.
Samozřejmě platí, že součet všech zářičů různé frekvence je roven celkovému počtu všech zářičů. Tudíž platí rovnice

Použijeme tuto rovnost pro výpočet neurčeného činitele a, úhrnnou energii přitom klademe rovnou 1.

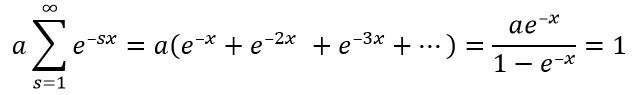
V uvedené rovnici se jedná o součet nekonečné řady členů s kvocientem q = e^–x. Jelikož je |q| < 1, geometrická řada má součet jak je uveden. Nekonečná geometrická řada se vyznačuje tím, že následující člen v její řadě se rovná předcházejícímu členu vynásobenému kvocientem q, v čitateli stojí první člen součtu a ve jmenovateli součtu stojí kvocient. Pro a tak dostáváme

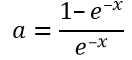
Pro střední hodnotu zářivé energie bude:

Toto není geometrická řada, jelikož členy jsou násobeny číslicemi 2, 3, atd. Vyzrajeme nad tím tak, že namísto násobení sčítáme členy 2, 3, n krát, čili

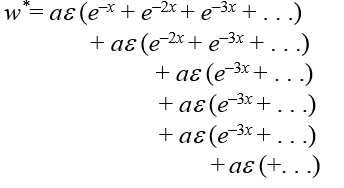
Nyní již všechny nekonečné součty jsou nekonečné geometrické řady a lze vyjádřit jejich součet.

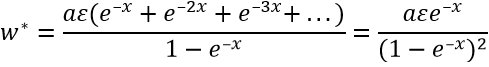
Dosazením sem výše uvedené x = ε/kT , a = (1 – e^–x )/ e^–x , ε = hf, obdržíme

Jak jsme výše uvedli, klasická teorie záření uzavřené dutiny vede k rovnici E_0λ = 2πcw*/λ⁴. Dosadíme-li do ní střední hodnotu w* podle Planckovy kvantové teorie a za kmitočet f = c/λ, obdržíme rovnici

Teď už můžeme psát podle zvyku raných matematiků
Q.E.D – quod erat demostrandum (což mělo být dokázáno).

Planck objevil kvantovou podstatu přírodních jevů a zahájil vznik nových teorií a technických vymožeností na základě kvantové teorie. Kromě toho objevil ještě Einsteina, jehož stať Zur Elektrodynamik bewegter Körper z roku 1905 [2] (O elektrodynamice pohybujících se těles) natolik ocenil, že jejímu autorovi pomohl ke kariernímu růstu. Einstein se stal z drobného úředníka švýcarského patentového úřadu v Berně řádným členem akademie a řádným profesorem univerzity v Berlíně.

Ve své stati Einstein odhaluje revoluční změny v chápání přírody. Mělo se za to, že plynutí času je invariantní, to znamená, že nezávisí na rychlosti zdroje světla ani na rychlosti jeho příjemce. K vysvětlení záporného výsledku přelomového Michelson–Morley experimentu z r. 1887 Einstein usoudil, že plynutí času není invariantní, ale rychlost světla je invariantní. Je to jeden z postulátu speciální teorie relativity. O tři měsíce později uveřejněný Einsteinův článek obsahuje odvození slavné rovnice E = mc², která vyjadřuje ekvivalenci hmotnosti a energie.

Do třetice ještě v roce 1905, při studiu vnitřního fotoefektu látek, Einstein objevil foton. Byla to nová mikročástice, která má energii

E_f = hf,

kde h je Planckova konstanta a f je kmitočet světla (záření). Foton vykazuje také hmotnost a jako korpuskuli Einstein mu dal konkrétní fyzikální obsah (pojem korpuskule zavedl Newton ještě na konci sedmnáctého století, když světlo považoval za proudění korpuskulí, ale neřekl co korpuskule je). Foton spojuje vlnovou teorii s korpuskulární.

Po těchto úspěších není se čemu divit, že Planck Einsteina vysoce cenil a protěžoval ho v kariéře.

Začátkem dvacátého století si fyzikové stěžovali na vtipně řečené dilema, v pondělí a uterý vysvětlujeme záření podle vlnové teorie a zbývající dny podle korpuskulární. Toto dilema v roce 1924 vyřešil Luis de Broglie (vyslovuje se „de Broj“) , když přišel s nápadem, že veškerá hmotná tělesa, o kterých uvažujeme jako o korpuskulích (elektrony, fotbalové míče atd.), vykazují zároveň vlnové chování o vlnové délce

λ = h/p
vlnová délka = Planckova konstanta vydělena hybností.

Byla to natolik fantastická představa, že když ji de Broglie předložil ve své disertační práci, zkušební komise byla na rozpacích udělit mu akademický titul. Naštěstí komise byla tak rozvážná, že jednu kopii disertace poslala Einsteinovi na posouzení. A ten dal kladný doporučující posudek. Svoji disertaci de Broglie obhájil. V roce 1927 fyzici Davisson a Garmer z USA a Thomson ze Skotska prokázali vlnové chování elektronu. Všichni jmenovaní fyzici spolu s de Brogliem získali v roce 1927 Nobelovu cenu [3].

Tak se zrodila kvantová mechanika.

Na základě de Broglievovy teorie dualismu částice-vlna Schrödinger odvodil rovnici:

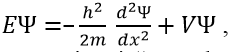
kde E je celková energie elektronu hmotnosti m, jež se pohybuje ve směru x, kde působí potenciál V, h („přeškrtnuté h“) je Planckova konstanta h vydělena 2π, a nakonec řecké písmeno psi ψ označující pravděpodobnost výskytu částice.Schrödinger odvodil svou rovnici ve snaze chápat elektron jako vlnu ψ podle de Broglieho dualizmu. Podobně jako struna houslí může kmitat jen na určitých vlnových délkách, také vlna elektronu ψ může nabýt jen určité vlnové délky, a teda určité kvantované energie. M. Born usoudil, že vlnu ψ je třeba interpretovat jako pravděpodobnost výskytu elektronu v bodě x, a tím pádem z vlny se znovu stala korpuskule, jak to umožňuje de Broglieho dualismus.

Tak se zrodila vlnová mechanika.

Schrödingerova rovnice sehrála rozhodující úlohu v teorii tranzistoru [5], který v letech 1947–1948 vynalezli John Bardeen, Walter H. Brattain a Wiliam Shockley – Nobelovu cenu obdrželi v roce 1947. V roce 1959 J. S. Kilby patentoval první integrovaný obvod, který obsahoval sice všeho všudy jen tři součástky, ale od té doby počet součástek na čipu obvodu ročně exponenciálně narůstá. Kilby Nobelovu cenu obdržel v roce 2000. Dnes již každé dítě ovládá mobil a netuší, že v ruce drží integrovaný obvod s nespočetným množstvím tranzistorů.

Další krok v rozvoji teorie mechaniky učinil P. A. M. Dirac, když v roce 1928 uveřejnil svou relativistickou vlnovou rovnici [4].

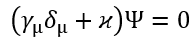
Odpustíme si vysvětlení jednotlivých veličin v rovnici a omezíme se jen na konstatování, že v ní je zúročena Einsteinova relativita a Schrödingerova rovnice. Z Diracovy rovnice vyplynulo, že kromě elektronu existuje ještě částice se stejnou hmotností jakou má elektron, ale má kladný elektrický náboj. Předpovězenou částici v kosmickém záření objevil C. D. Anderon a nazval ji pozitron. Nobelovu cenu obdržel v roce 1936. Dirac za předpověď neznámé částice Nobelovu cenu dostal již v roce 1933.

Tak se zrodila relativistická kvantová mechanika,

neboli QED – kvantová elektrodynamika.

*** Vidím-li dál, tak proto, že stojím na ramenou mých předchůdců (Newton). ***

Odkazy

[1] Z. Horák: Úvod do molekulové a atomové fyziky, SNTL, Praha 11, 1957
[2] A. Einstein, v Google take: On the electrodynamics of moving bodies.
[3] T. Hey a P. Walters: Nový kvantový vesmír. Nakladatelství Argo, Praha 3, 2005.
[4] J. Kvasnica: Priekopníci modernej fyziky, SÚV SZM, Bratislava, 1987.
[5] L. Szántó: Integrované obvody od pohyblivosti elektronu k mikro- a nanoelektronice, Google.