Objem kvádru y se matematicky vyjadřuje rovnicí

y = x (S – 2x) (V – 2x),
kde x je délka strany odstřihnutých rohů archu, S a V jsou šířka resp. výška archu, jejichž velikosti jsou uvedeny v zadání úlohy. Rovnici rozepíšeme, aby se další matematické úkony snadněji prováděly
y = 4x³ – 2x²(S + V) + xSV

Extrémní hodnotu y znázorňuje tangenta, která svírá nulový úhel s osou x.
Tangenta extrému y se nachází tam, kde derivace y podle x se rovná 0.
dy/dx = 0 = 12x² – 4x(S +V) + SV
To je kvadratická rovnice, která pro x vykazuje dva kořeny, tudíž y má dva extrémy.

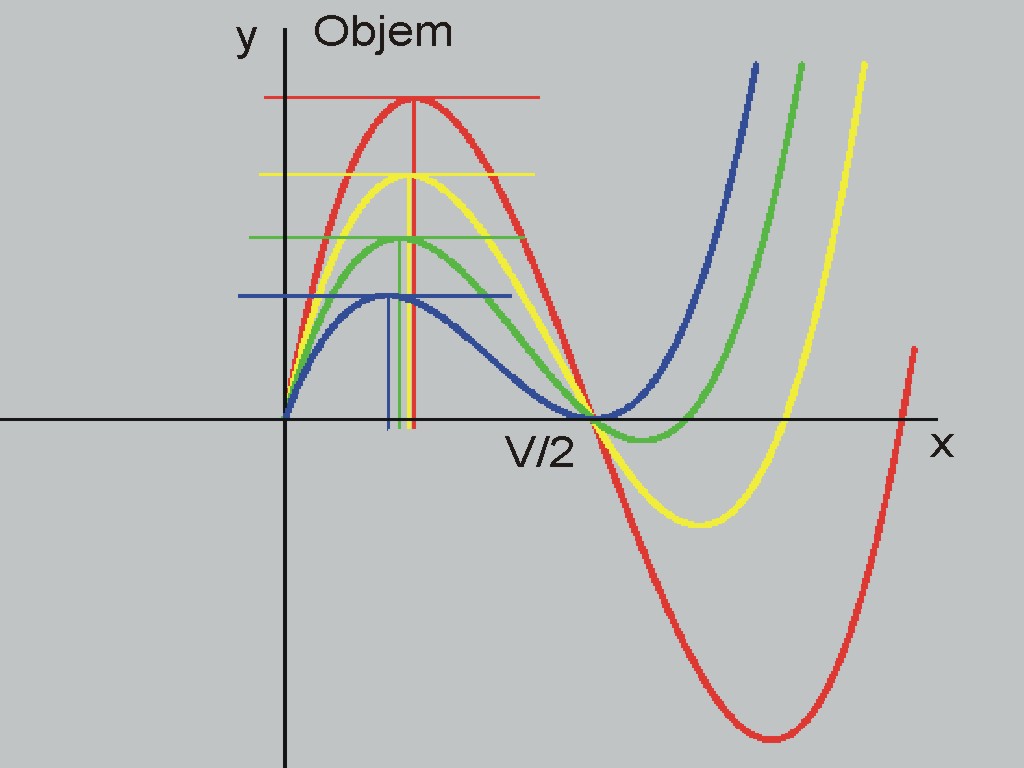
Obr.2 Rovnice objemu y = x (S – 2x) (V – 2x) pro x v mezích 0 < x < ∞
(kvadr.exe)

Grafický obraz rovnice y a tangenty v kladném extrému jsou znázorněny na Obr. 2. Pro každou hodnotu výšky archu V můžeme odstřihnout jen čtverečky kusů o maximální velikosti strany x = V/2, pak objem kvádru má nulovou hodnotu. Zbytek archu je menší arch.

Objem vykazuje dva extrémy – jeden kladný, druhý záporný. Záporný objem neexistuje podle zdravého rozumu, a tak použitelný je kladný extrém objemu, kde je znázorněna také tangenta. Matematice však nic nebrání znázornit y i pro další kladné hodnoty x. Tu se ukazuje první rozpor mezi zdravým rozumem a matematikou. Dřív než si tento rozpor objasníme a vysvětlíme v čem je rozdíl mezi zdravým rozumem a matematikou, uveďme ještě další možnosti matematiky.

Obr.3 Rovnice objemu y = x (S – 2x) (V – 2x) pro x v mezích –∞ < x < ∞
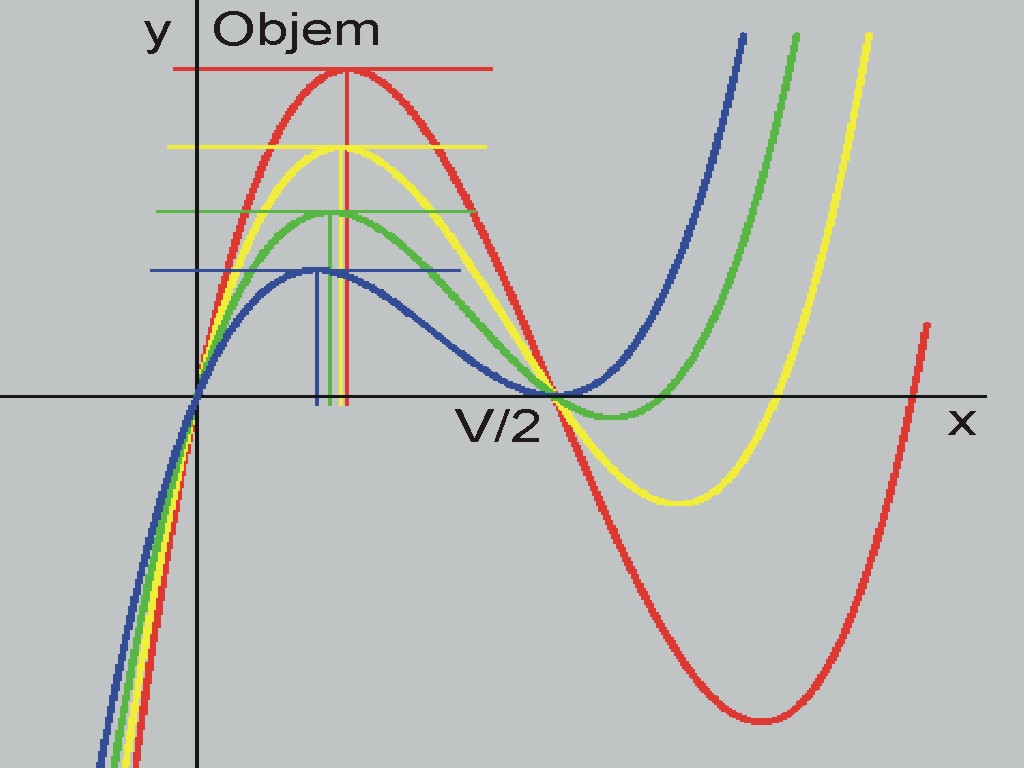
Rovnice objemu y je znázorněna i pro záporné hodnoty x, což podle zdravého rozumu není možné.
( Kvadr.exe)

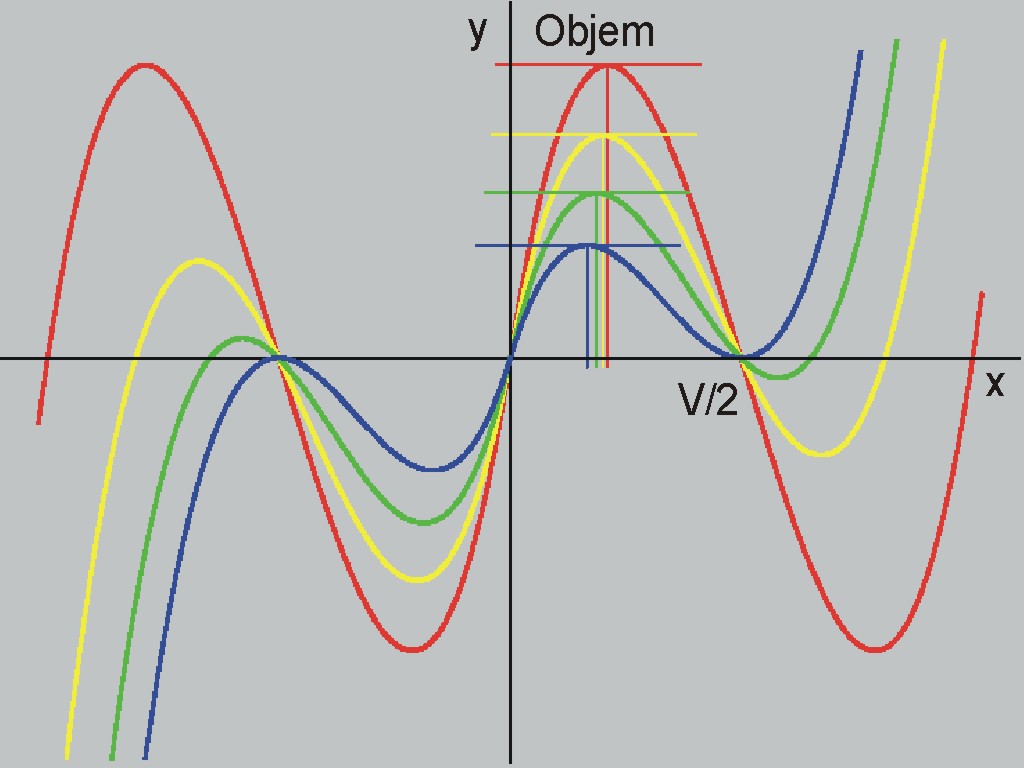
Obr.4 Rovnice objemu je y = x (S – 2x) (V – 2x) když x > 0 a také pro

y = x (–S + 2x) (–V + 2x) když x < 0

(Kvadr.exe)

Na rozdíl od Obr. 3 předpokládáme na Obr. 4, že pro záporné hodnoty x existuje záporný arch papíru, což podle zdravého rozumu není možné, ale matematika to umožňuje. Graf objemu y pro hodnoty x < 0 a graf objemu y pro hodnoty x > 0 jsou zrcadlové obrazy nejdřív podle osy y a pak podle x.

Po tomto předvedení možností matematiky vysvětlíme, v čem spočívá rozdíl mezi zdravým selským rozumem a matematikou.

Zdravý selský rozum se u člověka vytváří od útlého věku na základě objevování přírodních jevů pomocí smyslových orgánů: očí, uší, nosu atd. V pozdějším věku člověk získává poznatky studiem na škole a čtením knih. Nicméně smyslové orgány člověka jsou omezeny – ptáci mají lepší vidění, divoká zvěř lepší slyšení atd. I když moderní přístroje – mikroskopy, mikrofony atd. rozšiřují možnosti lidských smyslů, podstatné je, že pojmy, které jsou stavebním kamenem zdravého rozumu člověka, mají konkrétní fyzikální obsah. Vysloví-li se slovo např. jablko, vždy se nám vybaví jablíčko a ne nějaký meloun.

Matematika má také své pojmy jako je např. číslo, proměnná, vektor, matice atd. Podstatné je, že tyto pojmy nemají konkrétní fyzikální obsah. Matematika zkoumá jenom vzájemný vztah mezi pojmy. V rovnici y = x (S – 2x) (V – 2x) zkoumá jenom, jakých hodnot může proměnná y nabýt ve vztahu s ostatními pojmy v rovnici. Konkrétní fyzikální význam těmto pojmům a výsledkům matematických bádání pak dodatečně přidá člověk podle svého zdravého rozumu.

Na závěr těchto úvah o vztahu zdravého rozumu a matematiky dodejme, že grafy na Obr. 2 až Obr. 4 vyhodnocoval svým zdravým rozumem amatér (slovo je latinského původu slova amator – milovník). Někdy se vyplatí více důvěřovat matematice a hledat vysvětlení k zamítnutým výsledkům.

Uveďme klasický příklad objevení antihmoty. Významný fyzik Paul Dirac studoval z pozic kvantové relativistické mechaniky pohyb elektronu a odvodil rovnici. Její řešení má dva výsledky – jeden kladný, druhý záporný. Kladný výsledek by amatér připsal elektronu, záporný by označil za nepoužitelný. Ne tak Dirac, který důvěřoval matematice a hledal vysvětlení pro záporný výsledek. Došel k závěru, že existuje do té doby neznámá mikro částice a předpověděl, že existuje částice s hmotností jako elektron, ale s kladným elektrickým nábojem. Svou předpověď publikoval v roce 1928 a v roce 1933 byl poctěn Nobelovou cenou. Diracovu částici objevil v kosmickém záření C. D. Anderon a Nobelovu cenu za objev obdržel v roce 1936.

Dirac bádal a pátral po přírodních zákonech

a jediný „nástroj“, který k tomu měl byla matematika. Nezkoumal a nenavrhoval lidské artefakty jako např. kvádr vytvořený z archu papíru. Tam si vystačíme s rozvinutým zdravým selským rozumem.

Povzbuzeni Dirackovým příkladem, žertem si dovolujeme říct, že rovnice objemu pro záporné hodnoty x a záporný arch papíru (Obr. 4) má fyzikální význam. Objevili jsme záporný papír a čekáme jen na výrobce, který ho vyrobí a dá mu název, nejlépe řeckého původu.

Připomeňme si ještě jeden slavný vědecký výkon, kde matematika slavila triumf. V první polovině 19. století poslední známou planetou v sluneční soustavě byl Uran. Z astronomických pozorování se vědělo, že planeta se nepohybuje přesně po vypočítané dráze podle Newtonových zákonů. Byly chybné tyto zákony? Uznávaný astronom a matematik Leverrier jím pevně věřil a z vyhodnocení odchylek pohybu Uranu od vypočítaných hodnot dospěl k přesvědčení, že existuje do té doby neznámé astronomické těleso, které svou gravitaci odchylku způsobuje. Leverrier informoval astronoma Galleho, kde by se mělo neznámé těleso na obloze nacházet. Galle tam těleso skutečně uviděl a nová planeta dostala jméno Neptun.

A do třetice, E. L. Planckovi se matematickým „klíčem“ povedlo proniknout k jednomu z nejutajovanějších přírodních zákonů, ke kvantovému vyzařovacímu zákonu, který pak spustil lavinu nových přírodních a technických objevů. Připomeneme si je v závěreční kapitole.