Rok 1900 byl začátkem nejen nového století, ale i nebývalého pokroku v poznání zákonů přírody. Od pradávna myslitelé počítali s tím, že energie může nabýt jakýchkoli hodnot – že vykazuje spojité spektrum. Na základě studia záření tepla z černé díry a porovnáním klasické teorie záření s experimentem, objevil Planck kvantovou podstatu energie záření, a tak položil základy bádání přírody na základě kvantové teorie. Ve stávající kapitole uvedeme kroky, které vedou k Planckovu vyzařovacímu zákonu [1].

Obr.5 Černá díra

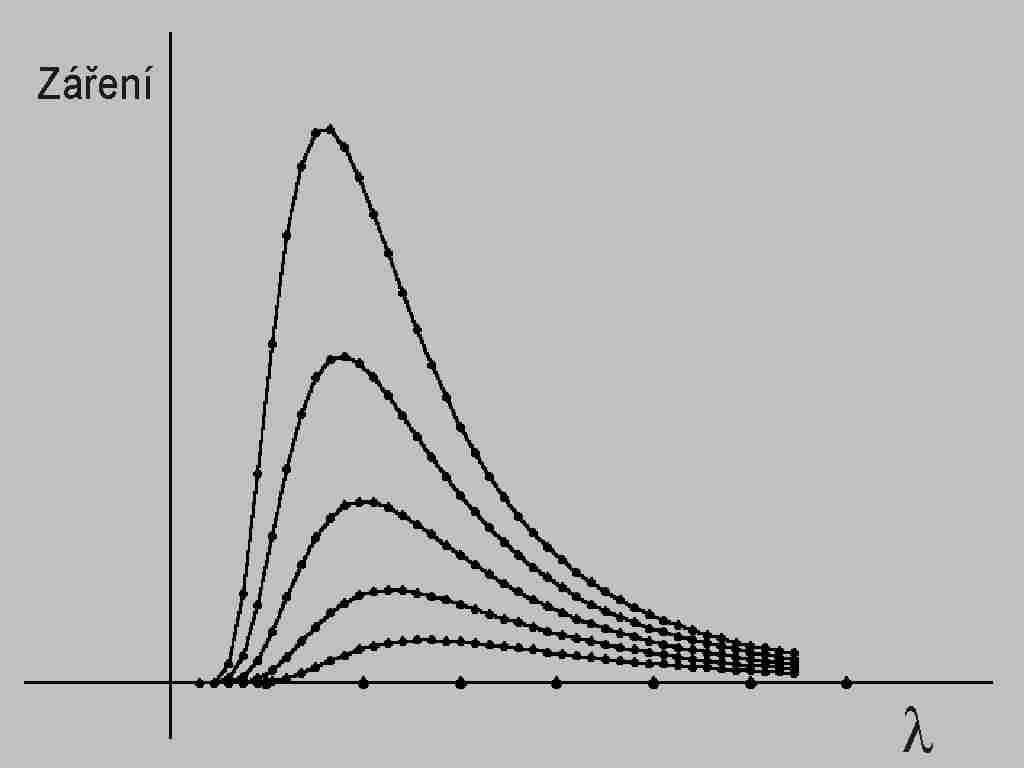
Obr.6 Grafické znázornění Planckova vyzařovacího zákona E_0λ od vysokých k nízkým teplotám.

(
Planck.exe )

Dle klasické statistiky zářivost uzavřené dutiny je dána rovnicí E_0λ = 2πcw*/λ⁴, kde c je rychlost světla, w* střední hodnota energií všech zářičů rozložených po vnitřní stěně dutiny a λ je vlnová délka záření. Tato rovnice, která vychází z předpokladu spojitého spektra vlnových délek, dává dobrou shodu s experimentem pro obor krátkých nebo dlouhých vlnových délek λ. V oblasti mezi těmito obory délek vln není shoda s experimentem. Shodu s experimentem Planck dosáhl teorií, podle které emise a absorpce zářivé energie může probíhat jen po celistvých násobcích kvanta ε = h.f , kde f je vlastní frekvence zářiče (zářivé energie) a h je Planckova konstanta h = 6,624×10^–24[Js].

Celkový počet zářičů je n. Pravděpodobnost, že zářiče emitují energii w_s, označme p_ws, přičemž s nabývá hodnoty s = 1, 2, 3……n. Z teorie klasické statistiky vyplývá p_ws = ae^–sε/kT , kde a je hodnota společná všem zářičům a k je Boltzmannova konstanta k = 1.380….×10^–23 [J/K], která vyjadřuje množství energie potřebné k zahřátí jedné částice ideálního plynu o jeden kelvin.

Počet zářičů s energii w_s je tedy n _s = nae^–sε/kT

a úhrnná energie W všech zářičů je:

Jelikož zářičů v černé díře je nespočetné množství, neděláme prakticky chybu, když počet všech zářičů n v rovnicích považujeme za nekonečný z matematických důvodů. Kvůli zjednodušení psaní následujících rovnic zavedeme označení x = ε/kT a tak bude
n_s = na e^–sx.
Samozřejmě platí, že součet všech zářičů různé frekvence je roven celkovému počtu všech zářičů. Tudíž platí rovnice

Použijeme tuto rovnost pro výpočet neurčeného činitele a, úhrnnou energii přitom klademe rovnou 1.

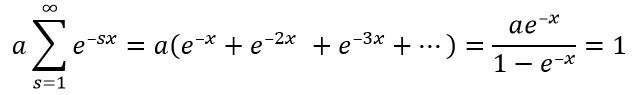
V uvedené rovnici se jedná o součet nekonečné řady členů s kvocientem q = e^–x. Jelikož je |q| < 1, geometrická řada má součet jak je uveden. Nekonečná geometrická řada se vyznačuje tím, že následující člen v její řadě se rovná předcházejícímu členu vynásobenému kvocientem q, v čitateli stojí první člen součtu a ve jmenovateli součtu stojí kvocient. Pro a tak dostáváme

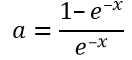
Pro střední hodnotu zářivé energie bude:

Toto není geometrická řada, jelikož členy jsou násobeny číslicemi 2, 3, atd. Vyzrajeme nad tím tak, že namísto násobení sčítáme členy 2, 3, n krát, čili

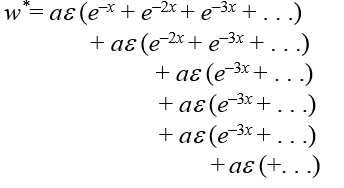
Nyní již všechny nekonečné součty jsou nekonečné geometrické řady a lze vyjádřit jejich součet.

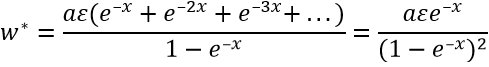
Dosazením sem výše uvedené x = ε/kT , a = (1 – e^–x )/ e^–x , ε = hf, obdržíme

Jak jsme výše uvedli, klasická teorie záření uzavřené dutiny vede k rovnici E_0λ = 2πcw*/λ⁴. Dosadíme-li do ní střední hodnotu w* podle Planckovy kvantové teorie a za kmitočet f = c/λ, obdržíme rovnici

Teď už můžeme psát podle zvyku raných matematiků
Q.E.D – quod erat demostrandum (což mělo být dokázáno).